Hi there! This blog series is intended as an intuitive explanation on Covariance Matrix Adaptation Evolution Strategy(CMA-ES) algorithm. I’m planning to divide the series into three parts. Part 1 skims over some background knowledge about Evolution Strategy(ES) in general. I used the otoro tutorial as a base when making part 1, so if you are already familiar with its content, you can skip to part 2.

part 2 & 3 will focus on the pseudocode from The CMA Evolution Strategy: A Tutorial page 29. If you have finished the otoro tutorial but then found the actual CMA-ES a little overwhelming (as I did), then you are at the right place!

pseudocode from The CMA Evolution Strategy: A Tutorial

Lets get started!

First of all, what is Evolution Strategy?

Covariance Matrix Adaptation Evolution Strategy(CMA-ES) hails from the family of Evolution Strategy(ES). ES is a family of algorithms inspired by evolution in nature, where individuals who are more adapted to their inhabited environments are more likely to get the opportunity to mate and produce offsprings. In short, “survival of the fittest”.

ES emulates this process into an optimization algorithm. The parameters to be optimized are encoded as “genes”, and during each generation, many individuals, each with a different set of “genes”, are generated and pitted against each other. Each individual gets a Fitness grade according to how well it performs, and the best individuals (elites) are those with the highest Fitnesses. Naturally, when generating offspring individuals for the next generation, high-fitness elites are given more weights.

But how are new individuals generated and how to give the elites more weights during this process? A simple method is through sampling from a normal distribution, with the distribution mean set to be the average of the “elite genes”, and the distribution std set as a hyperparameter. And if there is more than one parameter to be optimized (which is almost always the case), the sampling needs to be from a multivariate normal distribution where pretty much everything is in vectors or matrices, and std is replaced with covariance matrix.

What role does covariance matrix play in ES?

Covariance matrix can be a bit more involved to explain. But roughly speaking, just like how std controls the “flatness” of the probability distribution function shape in univariate normal distribution, covariance matrix controls the shape of the multivariate normal distribution. Maybe the the visualization below can help with your intuition. (You can run the script 2d_cov_demo.py from repo if you want to play around)

visualization of bivariate normal distribution; 2x2 covariace matrix on top right; circle represents line of equal probability density

Simple ES with fixed covariance matrix

Returning from covariance matrix to ES, we can build a very simple ES by iteratively updating the mean of an isotropic multivariate distribution with the mean of the elite “genes”(i.e. parameters). Maybe something like shown below. (run fixed_cov_es_demo.py)

visualization of ES with fixed covariance matrix; circle shows location and shape of distribution

A first attempt at adapting the covariance matrix

We can improve this simply ES by allowing the covariance matrix to adapt in such a way that “stretches” the distribution towards the optimum. Ideally, it should look like this.

what CMA-ES should look like

As a first step towards this ideal ES, the otoro tutorial describes a simple adaptation technique by using $E[(x_{elite} - m^{(g-1)})(x_{elite} - m^{(g-1)})^T]$ instead of $E[(x_{elite} - m^{(g)})(x_{elite} - m^{(g)})^T]$ during covariance matrix calculation. Notice how the former refers to the mean from the previous generation whereas the latter refers to the current generation mean. Intuitively, the former gives a covariance matrix that estimates selected (i.e. good) steps, which is the kind of information we want the algorithm to learn so it can continue making good steps in later generations.

This simple covariance matrix adaptation technique is a good starting point, but if we implement this simple technique as it is, the result doesn’t work very well. (run adapt_cov_demo.py)

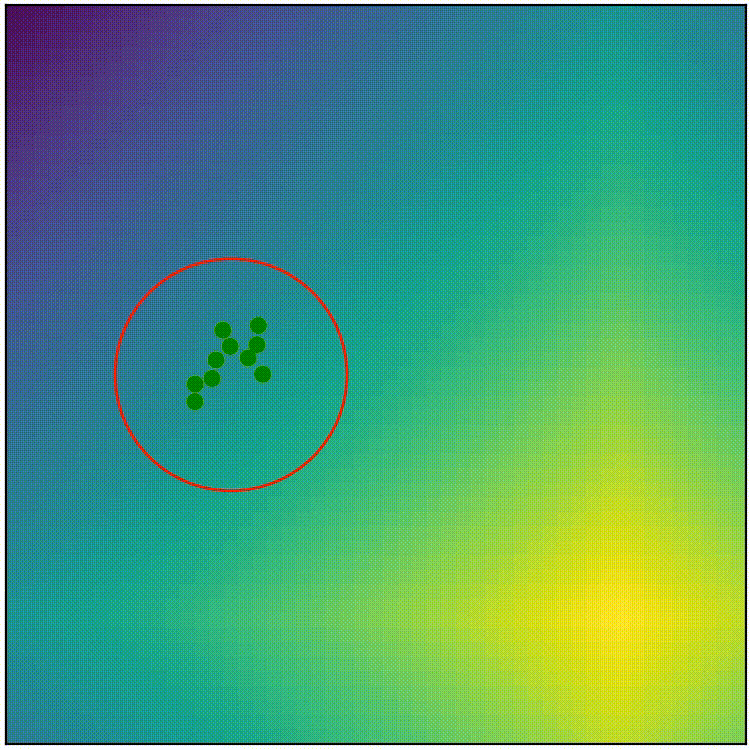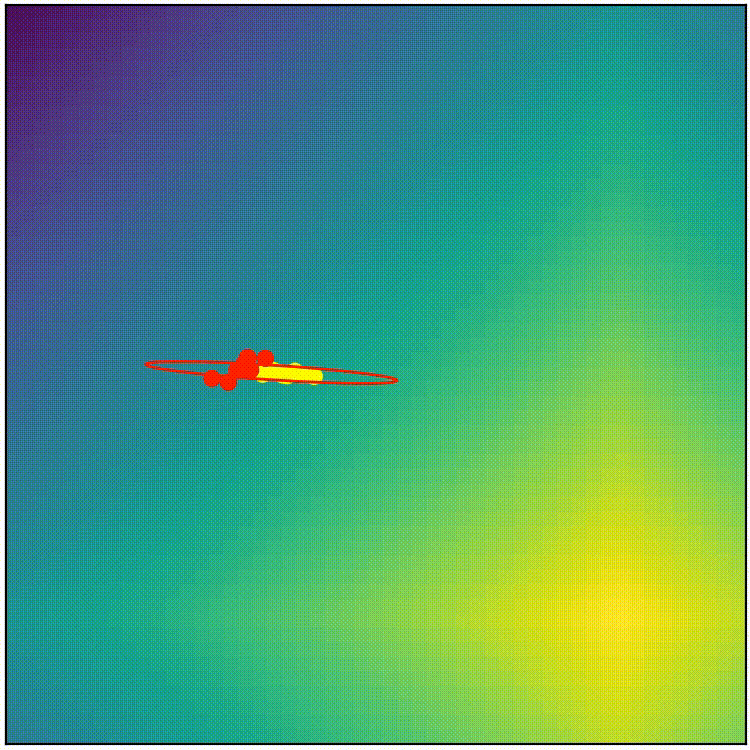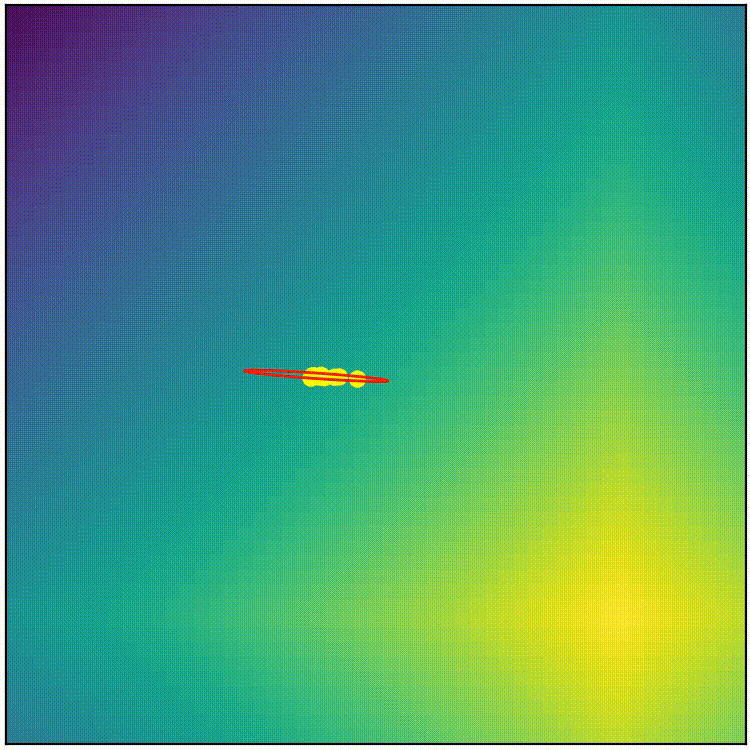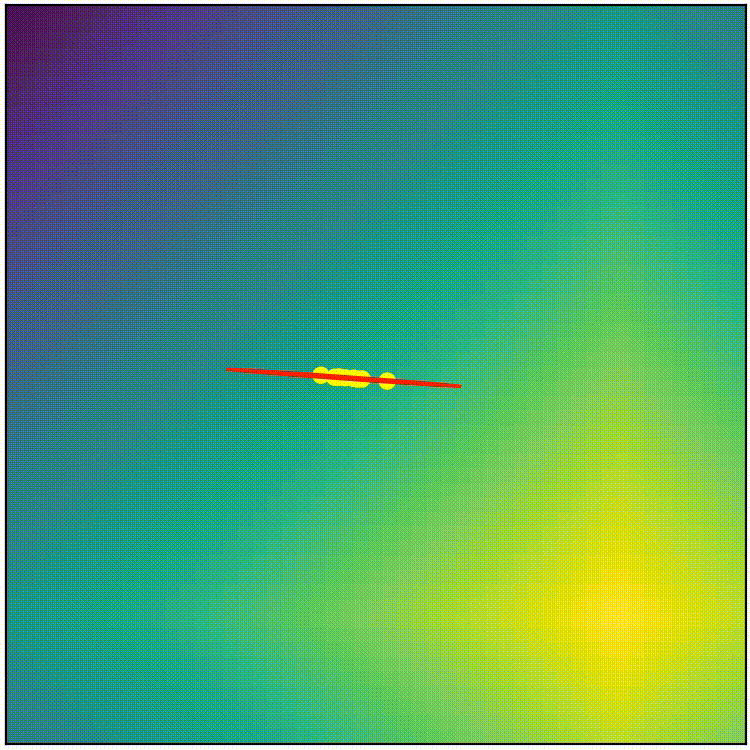simple covariance matrix adaptation doesn’t work very well

Here we can observe that, although the simple technique initially stretches the distribution towards high-fitness regions, the distribution soon becomes too thin to allow exploration in any other direction, so we end up with a local-optimum-like scenario. The “size” of the distribution also shrinks too quickly, which stalls the evolution before it can reach optimum. The simple covariance matrix adaptation is a good starting point, but it will require some refinement to become competitive. Before we proceed to the actual CMA-ES, here’s the pseudocode summaring what we have so far.

pseudocode: ES with simple covariance matrix adaptation

An interesting perspective on the role played by covariance matrix

If we go by the representation of normal distribution as an ellipse of equal probability density, then it’s not hard to observe that more individuals sampled from this distribution tend to lie somewhere near the long axis of the ellipse, especially if the ellipse is thin. Therefore, the average of elites, which determines the new mean, is also likely going to lie somewhere along the long axis. Moreover, if the ellipse has large radii, the sampled individuals are likely going to lie further away from the current mean, so the new mean is also likely to lie further away. Therefore, the direction and radii of the distribution ellipse is indicative of the direction and length of the update on mean. Following this intuition, we can almost say that the covariance matrix controls the exploration direction and step size of the optimizer centroid! (“almost”, because everything is probabilistic here) I found this visualization easier to understand than raw numbers.

Scripts used in this blog can be found at this repo. I also have a (badly recorded) series on Youtube that covers the content in this series.

Stay tuned for part 2!