CMA-ME: Using CMA-ES to guide MAP-Elites

Hi there! This blog follows up the previous blog on MAP-Elites, where we explored the idea of maintaining an archive of solutions that accomplish the target objective through a diverse set of behaviors. This was primarily motivated by the need to overcome local optima, but the archive could also be helpful for specific applications such as damage recovery. Here’s the MAP-Elites pseudocodes again:

Image from Mouret, J. B., & Clune, J. (2015)

For demo I implemented a simple MAP-Elites here and tried it on the quadruped Ant robot from QDgym, but the result we got was not great…

QDAnt best gait after 10000 generates of MAP-Elites

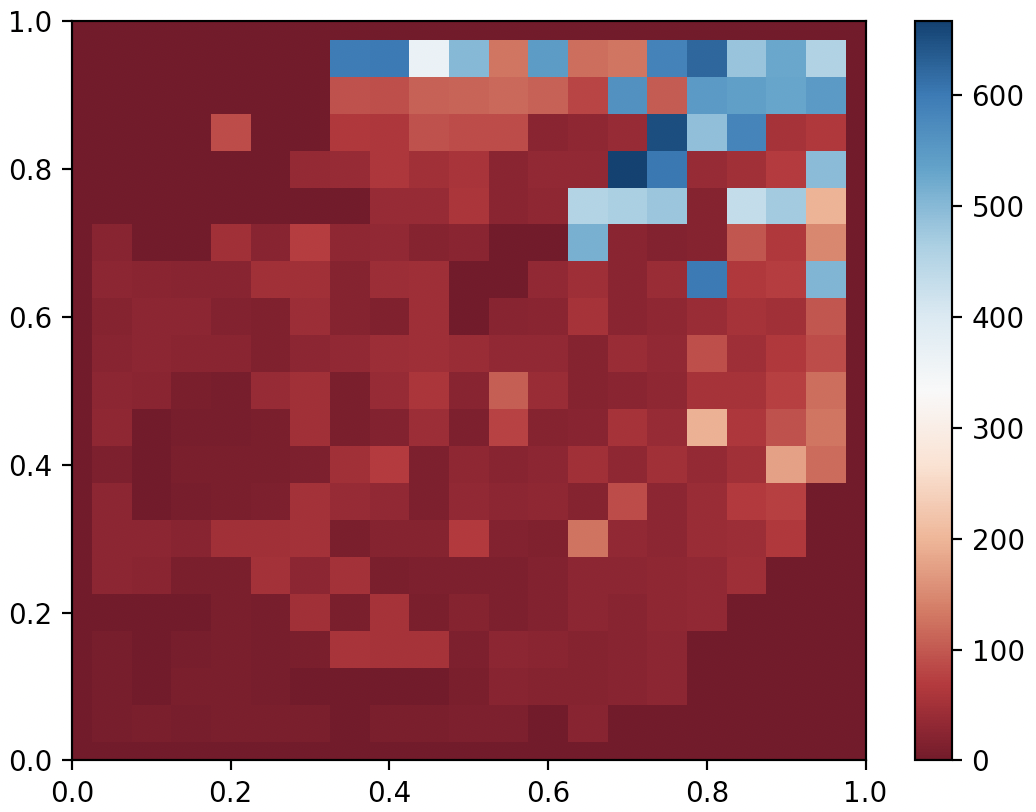QDAnt partial archive after 10000 generates of MAP-Elites

Of course, MAP-Elites was evolving many solutions simultaneously, and 10000 generations, taking about 20 minutes, would have been a modest budget even for Policy Gradient-based methods dedicated to finding just a single good solution. Moreover, we designed the controller to be a simple periodic gait that didn’t take advantage of any feedback…Ok…now that I’m done excusing myself, can MAP-Elites be made better? The answer is a resounding yes!

Previously we had been relying on simple mutation to evolve individuals. In other words, we would sample a non-empty cell randomly from the archive, and perturb the genome within it randomly by sampling $\sim N(genome, diag(\sigma^2))$. The new genome would be evaluated for its fitness and behavior descriptor, and would be added to the archive if either the archive doesn’t have its behavior descriptor, or if the archive has the behavior descriptor, but the corresponding old genome has lower fitness than the new.

Simple mutation (crossover is not much better) by isotropic Normal distribution isn’t ideal for this application. For a start, it’s difficult to choose a good standard deviation $\sigma$. We want large standard deviation in order to perturb the genome significantly enough to discover under-represented behavior descriptors, but in the mean time, genomes that are already doing relatively well need careful fine-tuning, i.e. small standard deviation. You could try hand-tuning standard deviation or design some kind of dampening as more behavior descriptors are discovered. That might get you past this first problem, with much tedious work, but even then, simple mutation is essentially blind when sampling new genomes. The only optimizing bias is applied by the archive when it discards genomes that are neighter new nor better, but otherwise MAP-Elites can only rely on “stumbling” upon a good solution – and just how likely is that? We are struggling hard enough with this simple 24-parameter setting ($[amplitude, frequency, phase]$ for each of the 8 joints), and there exist problems with millions of parameters!

Fortunately, using CMA-ES would give us both adaptive “standard deviation” and directionally-biased sampling. The maths can be pretty involved, and you can check out my 3-part series (part 1, part 2, part 3) if you are interested, but the general intuition is that we can sample multiple genomes, observe how high-performing genomes modify based on the current sampling mean, and modify the covariance matrix accordingly to try to reproduce those modifications. The idea of combining CMA-ES into MAP-Elites is introduced in Fontaine et al. (2020), and the resulting algorithm is known as CMA-ME. (Note: this blog may not reflect the latest CMA-ME since improvements have been made since Fontaine et al. (2020))

Whereas we used simple mutation, CMA-ME uses CMA-ES as the random_variation operator in MAP-Elites loop. Perhaps the easiest way to use CMA-ES on MAP-Elites is to simply use MAP-Elites as the archive of an independent CMA-ES optimization. In this case the CMA-ES instance is updated according to the raw fitness values of its samples, and the only interaction between CMA-ES and MAP-Elites is that the samples CMA-ES generates each generation are added to the MAP-Elites archive by the aforementioned criteria. When CMA-ES converges (i.e. when it finds an optimum and can no longer improve it), simply reset its mean to another random genome in the archive and re-initialize its states to the default start ($0$ for step size and both evolution paths, $diag(\sigma^2)$ for covariance matrix where $\sigma$ is a hyperparameter).

This approach can be effective at improving existing genomes in the MAP-Elites archive, but doesn’t really reflect the spirit of MAP-Elites, which is to find a diverse set of solutions. Although restarting from another genome is supposed to add some degree of diversity, in my experience I’ve noticed that CMA-ES tends to converge quickly – that is, without much exploration – when it restarts from a low-fitness genome, so in the end only the behavior descriptors associated with high-fitness genomes are explored, and we have a scenario similar to local optima.

In response to this problem, CMA-ME designs another mechanism that explicitly encourages exploration on random behavior descriptors regardless of fitness. It’s actually quite similar to the aforementioned approach, except that, instead of raw fitness, samples used to update CMA-ES are ranked by their alignment with a randomly chosen direction in the behavior space. Given a sampled genome and its behavior descriptor, the alignment is measured by the projection (dot product) of the genome’s behavior descriptor onto the behavior descriptor that was just randomly selected as the target direction. This way, CMA-ES will be motivated to explore behavior space along the chosen direction, with no consideration for fitness. When CMA-ES converges, this approach resets the mean and other states as before, but also select another random behavior descriptor as the next target direction.

The second approach can be seen as the exact opposite of the first since it’s effective at exploring new behavior descriptors, but ineffective at improving existing genomes. We can make them complement each other by switching between them through a scheduler. The scheduler described in Fontaine et al. (2020) keeps multiple CMA-ES instances in parallel, some updating and resetting by the first approach and some by the second approach, and switch among them round-robin style so each CMA-ES instance gets a turn generating samples and updating itself. Since the CMA-ES instances provide the samples to be evaluated, and potentially added, each instance is referred to as an emitter in CMA-ME. The CMA-ES instances optimizing for fitness are dubbed optimizing emitters, and those exploring along a random behavior descriptor dubbed random direction emitters.

Pseudocode from Fontaine et al. (2020); $generate$_$solution$ generates samples according to the current emitter $e$; $return$_$solution$ updates the current emitter’s CMA-ES instance according to the emitter’s ranking rules

Aside from these two emitters, Fontaine et al. (2020) also describes a third kind of emitters that simultaneously encourages both exploration of behavior space, and optimization of behavior descriptors already in the archive. Like the previous two kinds of emitters, it tempers with the ranking rule of samples during the CMA-ES update. Whereas optimizing emitters rank by fitness and random direction emitters rank by alignment with the target direction, this third kind of emitters rank by improvement over predecessor, hence they are dubbed improvement emitters. More specifically, each sample genome generated by CMA-ES is checked against the archive. If the archive doesn’t yet have its behavior descriptor, then the new genome is considered a massive improvement over what used to be nothing, and automatically ranked to the top. If the archive has its behavior descriptor, then improvement score is calculated by subtracting the old fitness from the new fitness, and samples are ranked by improvement score in descending order. By this criterion, samples with negative improvement (i.e. worse than their predecessors) would be ranked to the bottom, and you may also choose to not consider them at all, which accelerates CMA-ES convergence at the cost of not anti-learning bad examples.

Finally, I implemented a stripped-down version of CMA-ME based on the pycma package and my own simple MAP-Elites from the previous blog. I also made a minor addition by using sumtree (here’s a good tutorial) priority sampling when choosing the genome from which CMA-ES restarts. I used a single improvement emitter and my priority sampling was also biased with improvement score. All in all, the results were looking pretty good! Not only did CMA-ME manage to find what resembled interchanging swing and stance phases after merely 10000 generations, but it also found hundreds of almost-as-good variations! The codes can be found here, and on my 2017 Macbook Pro with no GPU acceleration, running 10000 generations took about 1 hour.

QDAnt best gait after 10000 generates of CMA-ME (Improvement)

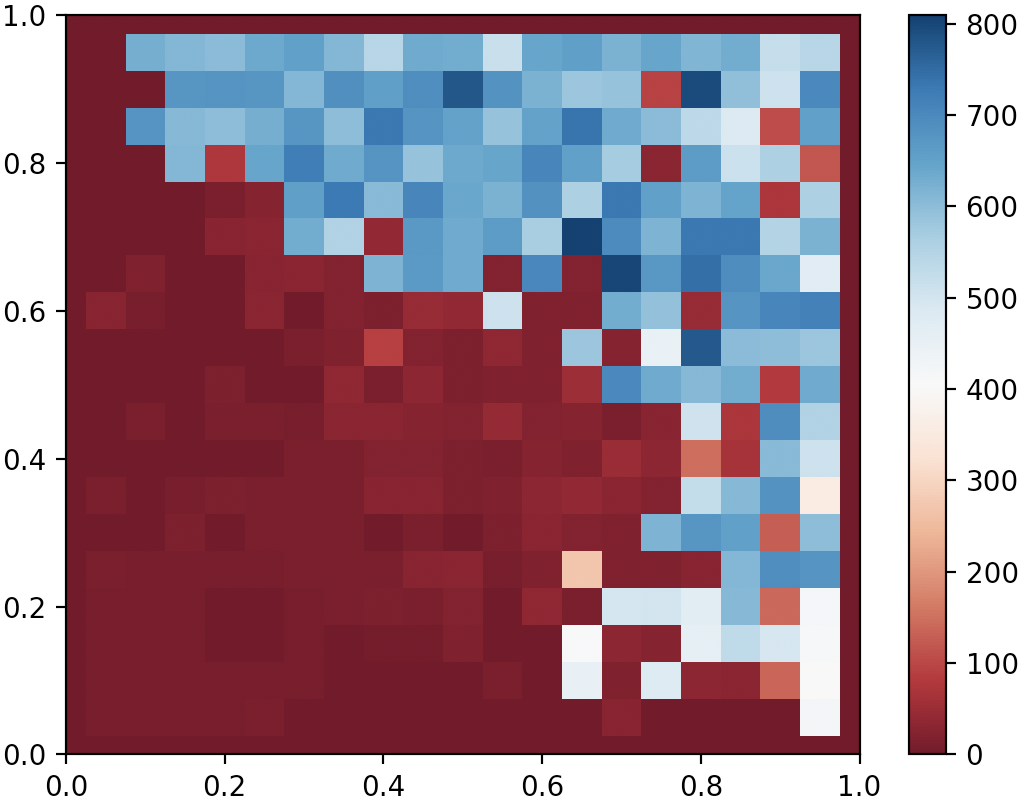QDAnt partial archive after 10000 generates of CMA-ME (Improvement)