Hi there! This blog showcases one of the many interesting applications of MAP-Elites algorithm. Namely, we’ll look at the paper Robots that can adapt like animals where the MAP-Elites archive is used for keeping “backup solutions” in case the optimum solution doesn’t perform as well as expected, thus allowing the robot to adapt to some degree.

This kind of performance drop can happen when, for example, the robot controller was trained in a simulated environment, but the real world turns out to differ from simulation, causing its performance to suffer. This is a well-known problem called Sim2Real (also known as reality gap), and has been the subject of many research projects such as Jakobi et al. (1995), Koos et al. (2012) and Tremblay et al. (2018). Aside from simulation error, another source of reality gap can be if the robot gets damaged during operation.

Either way, we want the robot to be able to bridge the gap between training environment and operational environment, which would obviously require trials in the operational environment. But there’s a twist – unlike in simulation, where we have access to conveniences such as being able to reset the environment, and being risk-free from robot damage, trials in real world don’t have these luxuries. Therefore real-world trials are more costly and dangerous, and the number of such trials should be minimized.

Given this requirement, we should prioritize trials that are likely going to contribute the most towards bridging the gap, but how do we figure out such trials? The methods vary depending on the context. In our case we have an archive of solutions evolved from CMA-ME (see my previous blog). Each of our archived solution is a relatively high-fitness solution within the constraint that it must use the four legs according to a different proportion. So each archived solution can be considered as a backup. If, for example, one leg gets damaged during operation, one of the other archived solutions that doesn’t use the damaged leg will not be affected as badly by the damage, and thus simply switching to this alternate solution might be a good recovery strategy!

In the aforementioned one-leg-damage scenario, if we know which leg is damaged, then we can directly instruct the robot to switch to the corresponding backup. This can be straightforwardly accomplished by engineering proprioception into the robot, but this is obviously a very restricted solution since it assumes too much prior knowledge and doesn’t work for damage scenarios outside of assumption. Another less restrictive way might be to rely on explicit self-diagnosis (e.g. Bongard & Lipson (2004)).

Both solutions rely on pinpointing the source of reality gap. By comparison, Intelligent Trial and Error (henceforth referred to as IT&E) doesn’t go through this intermediate step of trying to find the source, but chooses the replacement genome directly based on how well it is expected to perform. Initially we have only the archive from the training environment and have no information on the operational environment, so the first genome to be trialed will just be the best genome from the archive. But after this first trial we’ll have something to work with – since we know the new fitness of one genome, and can furthermore assume that similar genomes will perform somewhat similarly in the operational environment (though if you remember from the MAP-Elites blog, you may see that this assumption won’t work on genomes of complex encodings – but nevermind that for now). So we can update the tested genome with the new fitness, and also its neighbors with downscaled new fitness depending on the distance. If the genome we just tested doesn’t have satisfactory fitness, we can then choose from the updated archive the next likely candidate replacement, which will again be tested, and update itself and its neighbors accordingly.

But, perhaps counterintuitively, when choosing which genome to test, we don’t always prefer those with high fitness. It’s also a good idea to select genomes that are very different from any tested genomes, because we are less certain about their fitnesses, which might be surprisingly good! Or even if their fitnesses turn out to be bad, they will still illuminate their local neighborhoods which we previously know little about, so we’d know to stay away from similar genomes when choosing the next one to test. For these reasons, we need to balance between expected fitness and uncertainty when choosing which genome to test, and there’s a tool that perfectly matches this requirement.

Gaussian Process

There are plenty of good tutorials explaining gaussian process (I recommend the Youtube channel Gaussian Process Summer School), so I won’t re-invent the wheels. I’ll jump straight to what gaussian process provides for us – it learns a prediction of genome fitness while also giving a confidence interval about the prediction. i.e. $f(x) \sim N(\mu(x), \sigma^2 (x))$.

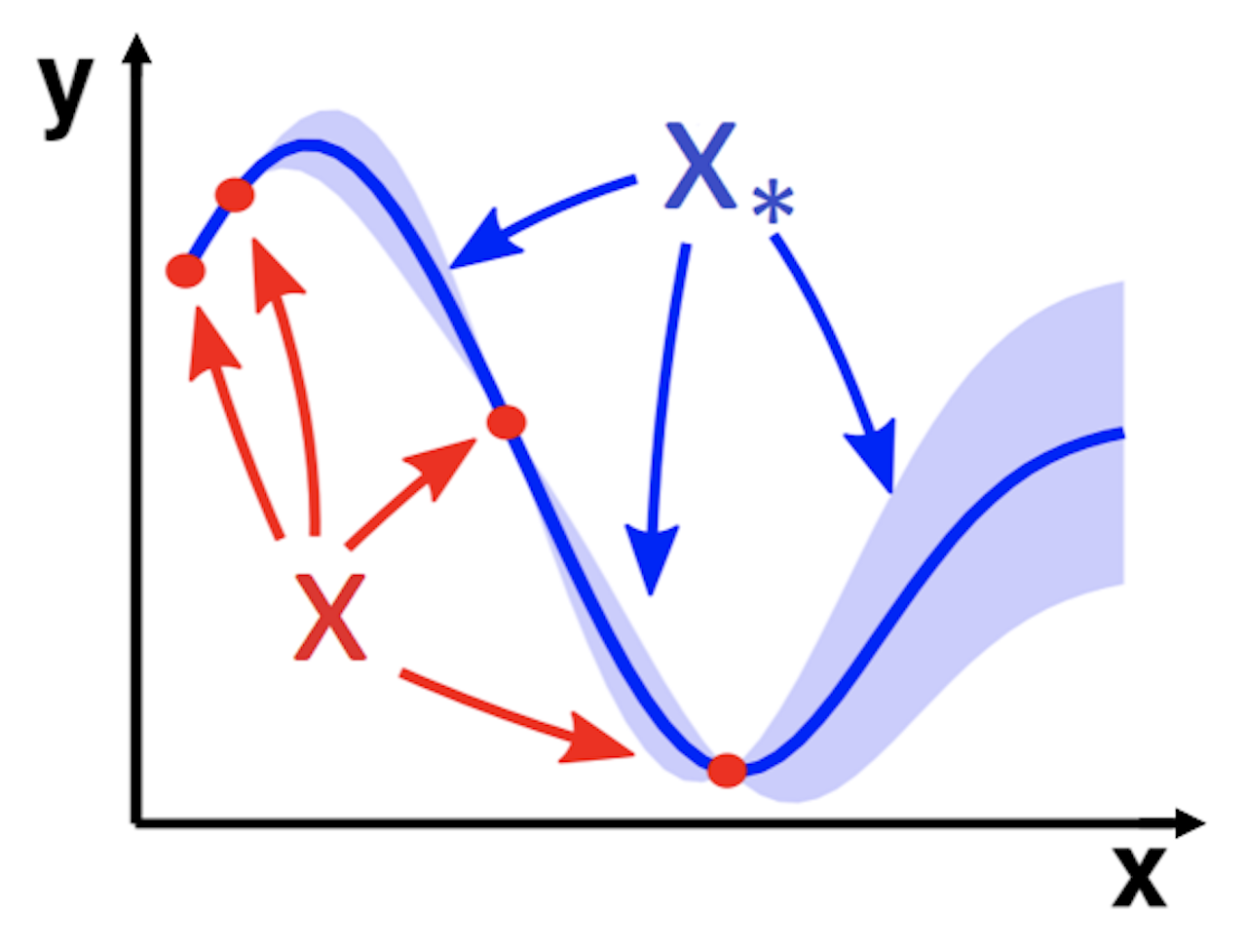Image from Wang, J. (2020); red dots are training data, blue line is the prediction, blue shade is confidence interval; notice how the interval widens going further away from training datapoints

It’s also worth noting that gaussian process in a non-parametric model where, roughly speaking, predictions are made based on the inputs’ similarity to datapoints in the training set (kinda similar to KNN). In a gaussian process model, its kernel $k(x, x’)$ determines the covariance between an arbitrary pair of datapoints $x$ and $x’$. Roughly speaking, if the covariance is strong, then similar datapoints will lead to very similar predictions, whereas weak covariance loosens this constraint, thus allowing a smoother model.

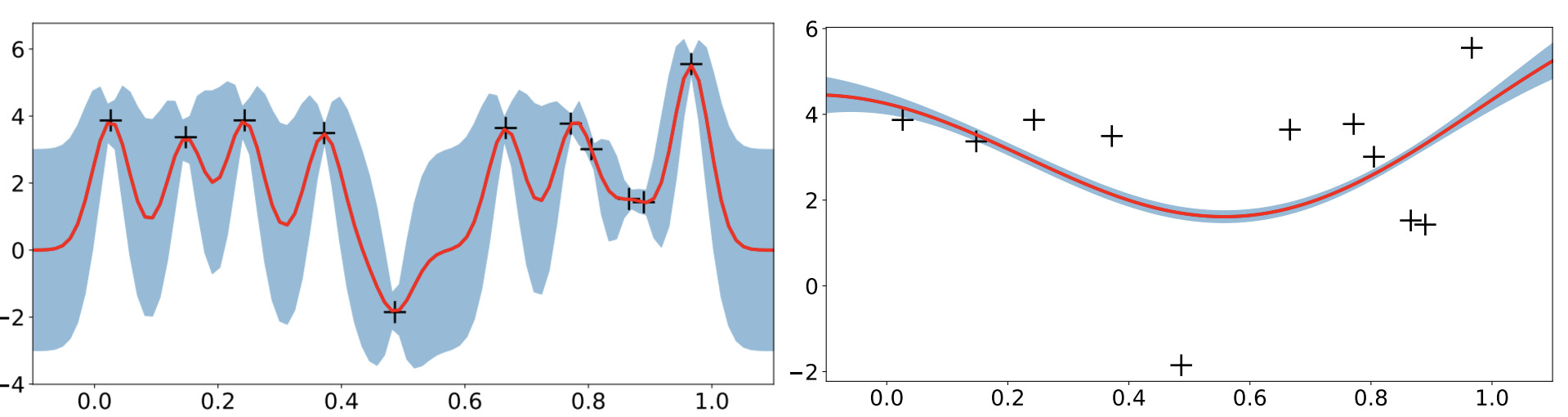Image from Wang, J. (2020); Left: kernel with strong covariance between similar datapoints; Right: kernel with weak covariance between similar datapoints

IT&E uses Matern 5/2 kernel as shown below. $\rho$ is a hyperparameter. Larger $\rho$ results in smoother model whereas smaller $\rho$ makes the model more “wiggly”.

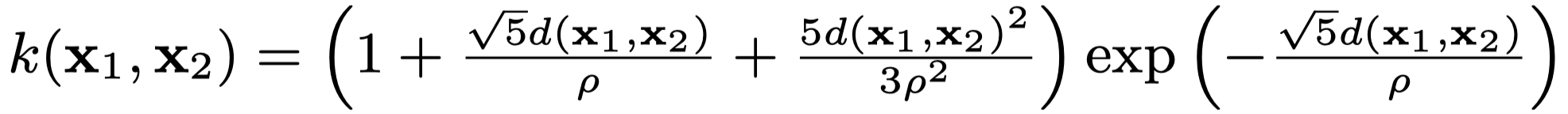Matern 5/2 kernel equation

Bayesian Optimization

The confidence interval provided by gaussian process gives us a way to balance between expected fitness and uncertainty: when choosing the next genome to test, we can use the criterion $x_{t+1} = argmax_x(\mu_t (x) + \kappa \sigma_t (x))$, where $\mu_t (x)$ is the fitness prediction, $\sigma_t (x)$ is the std. representing uncertainty, and $\kappa$ is a hyperparameter that determines the importance given to uncertainty.

Upper Confidence Bounds: choose the highest fitness after “padded” upwards with uncertainty

We will then use the fitness result we get from the test to update the gaussian process, which will again give us a genome to test…and the loop continues until we find a genome of satisfactorily high fitness. What I just decscribed was a typical bayesian optimization workflow, with Upper Confidence Bounds (UCB) as the acquisition function, testing in the operational environment as the evaluation function, and of course, gaussian process as the objective function. Also keep in mind that our gaussian process uses Matern 5/2 kernel, and we initialize its mean with fitnesses from the MAP-Elites archive.

Pseudocode

And there – we have an algorithm that intelligently chooses genomes from the archive to test in operational environment, until we decide we are satisfied with one of the re-tested genomes. The pseudocodes are shown below. The procedure is called M-BOA (short for Map-based Bayesian Optimization) rather than IT&E because IT&E also involves another submodule that builds up the archive (i.e. MAP-Elites), but since we already have the archive, this adaptation procedure is really all we care about.

Map-based Bayesian Optimization

Implementation

To mimic a damage scenario, I rigged the QDgym environment such that one of the eight joints doesn’t respond to inputs (If you observe the demo below you can see a hind leg always remaining vertical). I then run IT&E on the archive previously evolved with CMA-ME. After only 4 trials, IT&E was able to find an alternate controller for the damaged robot that achieved over 90% fitness of the undamaged robot. The codes can be found here. You’d want to mainly focus on mboa.py and recovery_agent.py.

90% recovery after merely 4 trials!

Below I show how the archive was updated during those 4 IT&E trials. Though take this with a grain of salt, because I only figured out how to show two of the four dimensions on a heatmap, so it doesn’t really reflect the archive accurately.

partial archive update during IT&E